Vuelve a caer en mis manos un libro coreano sobre haengma (pronunciado /henma/) y vuelvo a pensar cuanto se necesita este tipo de libros en occidente, junto con buenas colecciones de problemas de uso real en partidas.
A veces uno mira partidas de profesionales y no entiende nada, o a mitad de tus partidas tienes dudas entre varias jugadas. Ahí, un conocimiento de haengma es la clave para ser un dan o un kyu jugando.
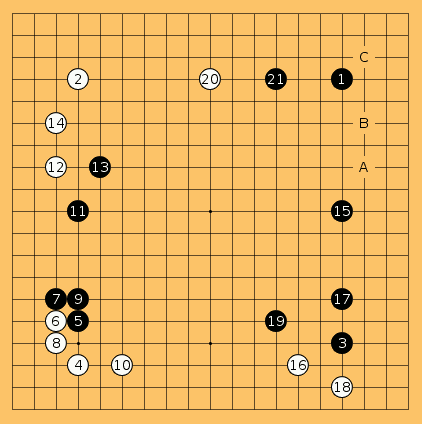
Por ejemplo, os muestro un diagrama de este libro, de nombre «Lecciones maestras de haengma de Cho Hunhyun (조훈현 행마법 특강)». Negro ha creado mucha influencia y blanco ha conseguido puntos. Por lo que blanco decide que es hora de invadir. Las opciones son A y B, pero se decide por A con la esperanza de más tarde aun tener la invasión en C disponible.
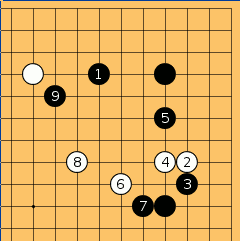Esta es la secuencia de invasión. A primera vista, lo normal es no entender casi nada. Hay tantas opciones donde jugar que la secuencia parece aleatoria, pero obviamente no lo es.
Las dudas nos asaltan: ¿Por qué negro al jugar 3 no defendió la esquina? ¿Por qué negro ha jugado 5 alta? ¿Por qué no jugo 5 en 6? ¿Por qué blanco 6 no se jugó en 7? ¿Por qué negro de pronto juega algo tan aparentemente lento como la jugada 7? Y así hasta el infinito.
Os dejo con el análisis interactivo:
;B[md];W[qh]
(;B[qi]LB[ph:A]C[Este es el punto de presion mas fuerte, evitando que blanco se deslice y amenazando jugar en A y con una forma muy fuerte bloquear a blanco]
;W[ph]C[blanco no tiene otra jugada]
(;B[pf]C[negro prueba el ataque mas fuerte]
(;W[ni]LB[pi:A][qj:B][qk:C]C[Blanco decide saltar pero presionando. Ademas, blanco siempre tiene la opcion de hacer el cambio de A por B. Pero si hace el cambio directamente, pierde la opcion de invadir en C. Asi que espera al momento correcto para jugar A o C, segun como siga la partida.]
(;B[oj]C[Negro amenaza el corte]
;W[lh]C[Blanco defiende el corte indirectamente y sale al centro]
;B[ke])
(;B[oh]C[Si negro intenta cortar…]
;W[pi];B[oi]
;W[qj]C[blanco consigue el lateral])
(;B[li]C[Si negro intenta bloquear el centro…]
;W[pi];B[qj]
;W[oj]C[La forma final de blanco (una «J») es muy fuerte]))
(;W[oj]C[En ocasiones, esta jugada al contacto es buena manera de luchar contra la forma diagonal de negro, pero en este caso falla]
;B[oi];W[pi]
;B[qj]TR[oi]C[ahora blanco no puede controlar la piedra negra marcada (la escalera no funciona) por lo que el resultado es nefasto])
(;W[nh]C[Si blanco simplemente salta al centro, sin creatividad…]
;B[nj];W[lh]
;B[lj]C[blanco no esta consiguiendo nada y negro crece mas y mas]))
(;B[ni]C[Si negro intenta cerrar por fuera…]
;W[qd]C[blanco puede intentar asaltar la esquina]
;B[qe];W[re]C[negro no puede controlarlo todo])
(;B[qf]C[si negro juega en 3a linea…]
;W[pf]C[blanco tiene una secuencia para crear forma de ojos]
;B[pe];W[rf]
;B[re];W[qg]
;B[qe];W[nh]LB[of:A][sg:B]C[blanco sale al centro, y ademas puede crear un ojo jugando en A o B]))
(;B[qe]C[Si negro defiende la esquina…]
;W[rj];B[qk]
;W[rk];B[rl]
;W[pi]C[Blanco se desliza por el lateral, gana algo de base y puede salir al centro con facilidad. Esta ultima jugada es clave para salir y ademas preparar el corte a negro.])
(;B[qj]C[Negro puede pensar en el pilar de hierro como solucion facil…]
;W[qd]C[pero entonces blanco asalta la esquina]
(;B[qc]C[si negro cede…]
;W[qe]C[blanco crea base con mucha facilidad])
(;B[qe]C[si negro se resiste…]
;W[re];B[rd]
;W[qc];B[rf]
;W[pe];B[qf]
;W[od];B[pf]
;W[oe]C[blanco acaba destrozando la esquina])))
Pingback: La mejor descripción de un problema | Badukaires
Si nos leyésemos a conciencia cada uno de los libros de Go que compramos otro gallo nos cantaría, jaja.
Este tiene muy buena pinta si explica todo así de bien.